Look at this thing I've just learned about Haskell!

Я нашел такой удивительный пример кода на Хаскеле, что мне захотелось о нем написать здесь. Вот эти две-три строчки кода:

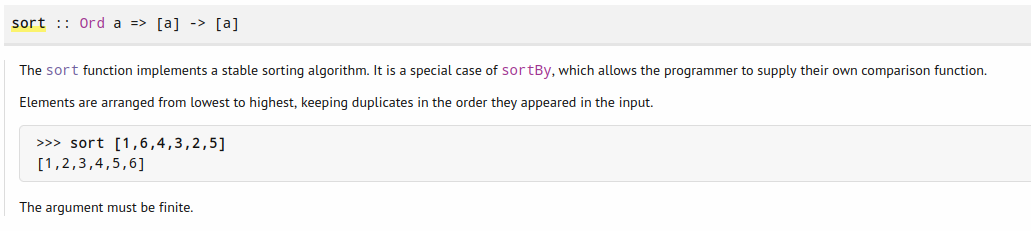
В Xаскеле есть то, что называется typeclass. По сути это интерфейс, который может реализовать ваш datatype, и это позволит использовать его в различных новых функциях. Пример typeclass - это Eq, для принадлежности к которому нужно определить функцию (==). Другой - Ord, для которого нужно определить оператор сравнения. Это, например, требование для элементов списка-аргумента функции sort:

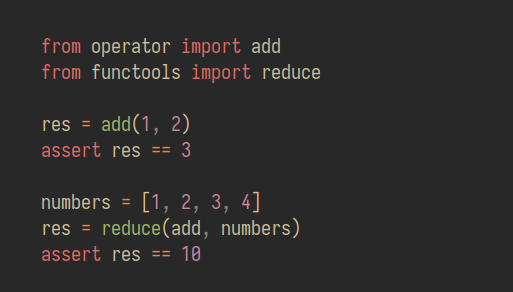
Итак, код выше - дефолтная реализация функции foldr для typeclass'а Foldable через функцию foldMap. Иными словами, чтобы принадлежать классу Foldable, можно просто реализовать foldMap. Foldable - класс типов, для которых определена свертка - просто применение бинарного оператора для получения одного результата. Пример левой свертки на Python:

Разумно полагать, что реализации foldr (правой свертки) хватает для принадлежности к классу Foldable. Однако как реализация странной функции foldMap позволяет реализовать foldr, а значит, принадлежать к этому классу? На самом деле, реализовать можно только одну из этих функций, а реализация по умолчанию второй позволит определить принадлежность к классу. Взглянем на сигнатуру функции foldMap (как я сказал, foldMap имеет дефолтную реализацию через foldr):

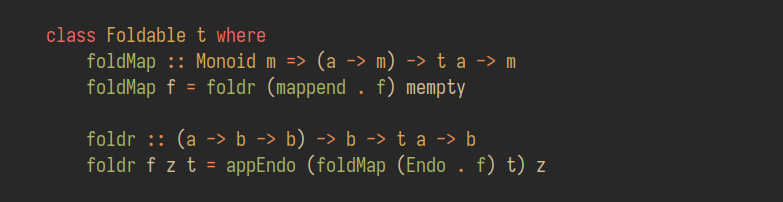
В foldMap :: Monoid m => (a -> m) -> t a -> m Monoid m означает что тип m принадлежит классу Monoid. Далее определяется функция с сигнатурой (a -> m) -> t a -> m, что означает, что функция foldMap принимает как аргумент функцию из типа а в тип m, т.е. (a -> m) и Foldable, содержащий тип a, а возвращает объект типа m класса Monoid. Иными словами, реализация этой функции должна, имея способ преобразовать элементы Foldable в моноид - некую функцию f :: (a -> m), как-то свести весь Foldable к одному элементу. Для простоты можно думать о ,Foldable как о списке или коллекции объектов, так как список, очевидно, является Foldable, (хотя не все реализации Foldable содержат множество элементов, см. Maybe). Из курса общей алгебры мы знаем, что моноид - алгебраическая структура со следующими правилами: замкнутость, ассоциативность, наличие нейтрального элемента. Примерно так и определен класс Monoid в Xаскеле:

mempty - нейтральный элемент, mappend - внутренний закон композиции моноида. Примеры моноидов в Xаскеле: Sum a - буквально числа со сложением, [a] (списки) - тоже моноид с оператором конкатенации ++. Таким образом мы можем просто скомпозировать все элементы нашего Foldable под действием функции (a -> m).
Возьмем двоичное дерево (каждая вершина либо пустая, либо имеет двух сыновей того же типа):

Вот пример реализации foldMap:

Мы рекурсивно применяем foldMap к левому и правому поддереву и композируем моноиды (функция f принимает вершину и возвращает моноид) из левого поддерева, текущей вершины и правого поддерева. База рекурсии - пустая вершина, для которой возвращается нейтральный элемента моноида. Таким образом, все дерево было скомпозировано в один элемент моноида.
Теперь мы готовы к тому, чтобы разобрать то, что меня так поразило - реализацию функции foldr. Вот она еще раз:

Вся суть скрывается в функции Endo. Endo - тип класса Monoid. Название объясняется тем, что Endo - моноид эндоморфизмов (проще говоря, функций типа (a -> a), собственно, так же, как и эндоморфизм является отображением из множества в (подмножество) себя). Довольно просто понять, что эндоморфизмы с оператором композиции функций является моноидом (замкнутость, ассоциативность тривиально доказываются, нейтральный - id, или f(x) = x). На самом деле, Endo такая же функция, как и любая другая, только она принимает на вход функцию и возвращает объекты типа эндоморфизм, который можно композировать с другими эндоморфизмами по закону этого моноида. Такие функции называются конструкторами типов. В данном случае конструктор типа единственный и называется так же, как и сам тип. Можно считать, что Endo - такая обертка вокруг функции (a -> a), которая сопровождается операцией композиции mappend и прочими функциями моноида. На данном этапе нужно вспомнить одну из важнейших концепций Хаскеля - currying (названо в честь того самого Хаскелла Карри). На самом деле, все функции в Хаскеле принимают один аргумент. Функции типа (a -> a -> a) (как функция, которой мы делаем свертку, например) сначала принимают в себя единственный аргумент и возвращают функцию, которая принимает "следующий", отсюда такая, казалось бы, странная нотация. Поэтому мы можем делать такое:

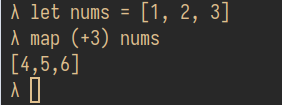
Здесь функция + (да, это функция) применяется к 3 и возвращает функцию (a -> a), которая прибавляет 3 к своему (единственному) аргументу, а map применяет ее ко всем элементам списка. Итак, вернемся к реализации foldr. Endo можно скомпозировать (. - это композиция) c бинарной функцией, которой нам нужно сворачивать. В результате действительно получается функция Endo, примененная к результату f в foldr. Какой же результат f? Из-за currying f после применения к объекту типа a возвращает другую функцию (a -> a), из которой и конструируется наш эндоморфизм. Таким образом, foldMap получает в себя Endo . f и из каждого элемента Foldable получает эндоморфизм. После этого foldMap композирует по закону моноида Endo все функции, то есть получает одну-единственную функцию - композицию всех - функцию типа (a -> a).

appEndo просто "извлекает" функцию из конструктора типа Endo. Потом эта функция-композиция всех функций применяется к начальному элементу z, что на выходе дает элемент типа a. Почему это верная реализация правой свертки? Продемонстрируем на примере. Допустим, есть список nums = [2, 4, 5] и бинарная функция (+). Мы делаем foldr (+) 0 nums. Предположим, что этот foldr использует реализацию по умолчанию, тогда (+) применяется к 2 и получается (2+); (2+) композируется с (4+), полученным таким же образом и скомпозированным с (5+). Такая функция, которая сначала прибавляет 5, потом 4, потом 2, применяется к нулевому элементу и получается (2 + (4 + (5 + 0))), что явно выглядит как правая свертка.